
![]()
![]()
מבחני התכנסות - מבחני השורש (קושי) |
|
|
|
|
|
|
הוכחה |
|
|
נתון הטור |
|
|
הוכחה |
| |
|
|
|
הוכחה |
![]()





 כאשר an
כאשר an 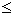 0
0 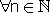
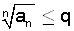 אזי הטור מתכנס
אזי הטור מתכנס 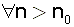
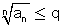
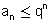
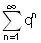 טור הנדסי מתכנס
ולכן ע"פ משפט השואה ראשון הטור
טור הנדסי מתכנס
ולכן ע"פ משפט השואה ראשון הטור 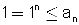 עבור אין סוף n -ים
עבור אין סוף n -ים 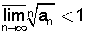 אזי הטור מתכנס
אזי הטור מתכנס 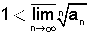 אזי הטור מתבדר
אזי הטור מתבדר 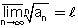 עבור הסדרה
עבור הסדרה 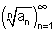 ויהי
ויהי 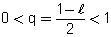
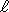 בסתירה להגדרת
בסתירה להגדרת 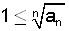 ומתקיים ב של נוסח 1
ומתקיים ב של נוסח 1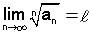 בהנחה שהגבול קיים
בהנחה שהגבול קיים 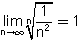 וכן
הטור
וכן
הטור 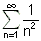 מתכנס
מתכנס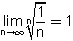 אבל הטור
אבל הטור 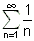 מתבדר
מתבדר
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©