|
|
|
| |
סדרות |
 |
סדרה - רשימה מסודרת של מספרים
, בה יש ראשון ,שני וכו' ללא סוף
|

|
למשל:
קבוצת המספרים הטבעיים 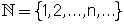 הינה סדרה
הינה סדרה
|

|
הערה:
קבוצת השלמים 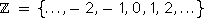
המסודרת ע"פ גודל אינה סדרה מכוון שאין לה איבר ראשון
שתי קצוותיה שואפים לאין סוף
אבל אפשר לסדר אותה כסדרה כך שיהיה איבר ראשון, שני וכו'
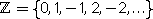
|

|
ההבדל בין סדרה לקבוצה:
בסדרה -
- חייב שיהיה איבר ספציפי המוגדר כאיבר ראשון של הסדרה
- יש חשיבות לסדר האיברים (ראשון שני וכו')
- איבר יכול להופיע מס' בלתי מוגבל של פעמים כגון :1,1,1,1,
|
| |
סדרה נסמן ע"י 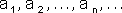 =
= 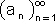
|
 |
סדרה קבועה - סדרה שכל
איבריה שווים זה לזה
באופן כללי :...c..c,c,c,c,c
ז"א 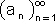 כאשר c =an
לכל n לעיתים מסמנים כאשר c =an
לכל n לעיתים מסמנים 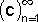
|
 |
סדרה הרמונית -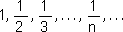
מתקיים כי  > >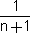 לכל n טבעי
לכל n טבעי
ואמנם 0< 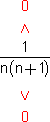 = = 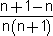 = =
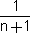 - - 
אומרים כי הסדרה יורדת ממש , חסומה מלעיל , יש חסם עליון והוא - 1
שהוא המכסימום
כמו כן  < 0 < 0
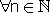
ולכן הסדרה חסומה מלרע - 0 הוא חסם תחתון שאינו מינימומם(לא שייך לסדרה)
|
 |
סדרות מונוטוניות:
נתונה סדרה 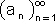
סדרה עולה - אם לכל n טבעי מתקיים an 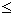 an+1
an+1
סדרה עולה ממש - אם לכל n טבעי מתקיים a
n+1 > an
סדרה יורדת - אם לכל n טבעי מתקיים an+1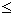 an an
סדרה יורדת ממש - אם לכל n טבעי מתקיים an
> an+1
|

|
דוגמאות:
1.הסדרה ההרמונית(ראה לעיל) יורדת ממש וגם
יורדת  >
> 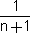 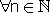
2.הסדרה הקבועה ...1,1,1,1,1 עולה כי :1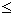 1 1 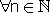
ויורדת כי :1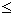 1 1 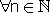
3.הסדרה ...,1,1,2,2,3,3 עולה אבל לא ממש
(אבל לא יורדת)
4.הסדרה ...,1,2,1.5,3,4,3.5 אינה סדרה מונוטונית
|
 |
כמעט כל - נתונה הסדרה 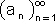
אנו נאמר כי " כמעט כל " איברי הסדרה בעלי תכונה P
אם לכל האיברים פרט למספר סופי יש התכונה P
|
 |
|

|
למשל : בטבעיים "כמעט כל"
איברי הסדרה גדולים מ-1265769
אבל לא נכון ש"כמעט כל" האיברים זוגיים |
|
|
|

![]()
![]()
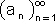 אנו נאמר כי " כמעט כל " איברי
אנו נאמר כי " כמעט כל " איברי ![]()





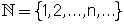 הינה סדרה
הינה סדרה 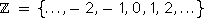
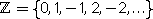
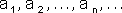 =
= 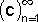
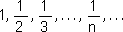
 >
>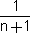 לכל n טבעי
לכל n טבעי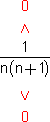 =
= 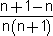 =
=
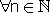
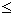 an+1
an+1  הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©