
![]()
![]()
טורים |
|||||||
|
|
|
||||||
|
|
למשל: |
||||||
|
|
סדרת סכומים חלקיים - מוגדרת ע"י:
|
||||||
|
|
טור מתבדר - אחרת |
||||||
|
|
הערה : אם הסס"ח מתכנס לגבול
אינסופי נאמר כי הטור מתבדר לאינסוף. |
||||||
|
|
|
||||||
|
|
סימון טור טור נסמן
ע"י "סיגמא"
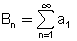 |
||||||
| |
|||||||
|
|
![]()





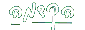
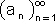 נרשום את איבריה באופן מפורש
נרשום את איבריה באופן מפורש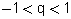
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©