
![]()
![]()
מבחני התכנסות - מבחני השוואה |
|
|
|
נתונים הטורים החיוביים |
|
|
הוכחה |
|
|
נתונים הטורים החיוביים |
|
|
הוכחה |
| |
|
|
|
הוכחה נוכיח את א ו-ג |
| |
![]()





 ו -
ו -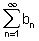
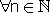
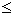 B
B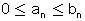 מתקיים
מתקיים 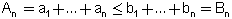
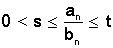
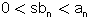
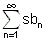
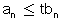
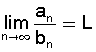
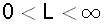 הטורים "חברים"
הטורים "חברים"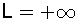 התכנסות
התכנסות 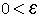 בפרט עבור
בפרט עבור 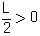 =
= 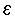
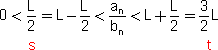
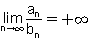
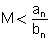 שזה גורר
שזה גורר
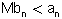
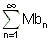 מתכנס
מתכנס 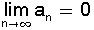
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©