|
אזי לסדרה יש גבול שהוא הגבול החלקי
|
|
נניח למקרה של - טענה: a גבול הסדרה יהי נתון האיברי הסדרה הוכחת הטענה:נניח בשלילה
שמחוץ ל - ( איברי הסדרה ע"פ משפט B - W המוכלל יש לאין סוף איברים אלו סדרה
חלקית בעלת גבול במובן הרחב :נאמר c, גבול חלקי זה של אין סוף האיברים הוא גם גבול חלקי
של 1.אם מדובר ב - 2.ע"פ אי שוויונים בסדרות
לגבי c נקבל a+ ולכן c
|
|
|
לסדרה יש גבול אם ורק אם an
= אם יש לסדרה גבול יחיד אז גבול עליון שווה לגבול תחתון
|
|
|
נראה למקרה ש - יהי a גבול חלקי כלשהו של ע"פ הגדרת גבול עליון וגבול תחתון נקבל an
ע"פ הנתון גבול עליון שווה לגבול תחתון ולכן הוא שווה ל - a לכן לסדרה יש גבול חלקי יחיד - ע"פ משפט קודם לסדרה יש גבול הערה: הוכחנו כי אם לסדרה יש גבול אז כל הגבולות החלקיים שווים לו |
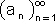יש גבול חלקי אחד ויחיד במובן הרחב 
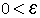נוכיח כי בקטע ( 
, 
)
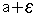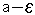נמצאים "כמעט כל "
,
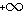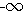
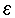
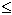c
או 
a וקיבלנו
במקרה זה גבול חלקי נוסף -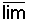 
an
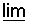
הצפיה
מומלצת ברזולציה ©
