
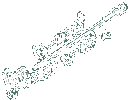
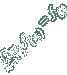
![]()
![]()
|
לכל סדרה אינסופית יש גבול עליון
וגבול תחתון
|
|
|
נתונה הסדרה bn הינה סדרת כל חסמי המלעיל של an: ז"א {...,b1 = sup{ a1,a2
הערה: b1 גדול
יותר/ שווה מ - b2 מכוון שיכול להיות ש - a1 bn תמיד קיים יתכן נדון רק במקרה ש - נתבונן בסדרה ז"א ע"פ משפט יורדת וחסומה הגבול
הוא חסם המלרע ל - וכן ידוע כי הגבול b הוא החסם התחתון אם כך (b = inf(bn וכן
b= נוכל לרשום {...,b = inf sup{ an,an+1 טענה
ראשונה: b הוא גבול חלקי של הוכחת הטענה: יהי {...,bk = sup{ ak,ak+1 ע"פ הגדרת
sup :לכל k טבעי קיים ank (אחד האיברים מ -
ak והלאה) כך ש -
bk - כשמגדילים את k ל - k+1 נבחר ank+1 כך ש - nk < nk+1 קיבלנו
סדרה חלקית המקיימת bk - על פי משפט
הסנדוויץ נקבל ank = b טענה שניה: b הוא הוכחת הטענה: יהי a גבול
חלקי כלשהו של ע"פ הגדרת גבול חלקי קיימת ל - נבחר {...,bnk = sup{ ank,ank+1
(החסם העליון של כל האיברים שאחרי קיבלנו ank הסדרה ראינו כי b= ראינו ank |
|
|
לכל סדרה יש גבול עליון
an
וגבול תחתון an המקיימים הסדרה יורדת ולכן הגבול שלה הוא האינפימום של המספרים
הכי גדולים ו -
הסדרה עולה ולכן הגבול שלה הוא הסופרימום של המספרים
הכי קטנים |
![]()
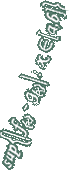



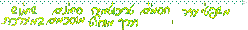


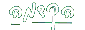
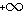 או
או 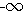 )
) 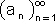 נסמן {...,bn = sup{
an,an+1
נסמן {...,bn = sup{
an,an+1
 {...,b2
= sup{ a2,a3
{...,b2
= sup{ a2,a3 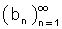 קל לאשר כי ...
קל לאשר כי ...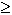 b1
b1 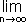 bn
bn
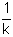 < ank
< ank 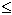 bk
bk
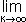
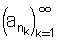 הגבול החלקי הגדול ביותר של
הגבול החלקי הגדול ביותר של 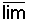
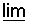
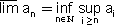
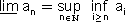
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©