|
משפט בולצנו ויירשטרס מספר 2 - B-W לכל סדרה אינסופית ולא חסומה מלעיל
(מלרע )קיים גבול חלק
|
|
1 אינו חסם מלעיל ולכן קיים an1 בסדרה כך ש - an1 > 1 גם ( max (an1 , 2 אינו חסם מלעיל ולכן קיים n1 < n2 an2 כך ש - (an2 > max (an1 , 2 נמשיך באינדוקציה ונקבל
|
|
|
(
)
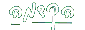
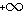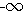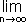
800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©
