
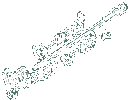
![]()
![]()
|
לכל סדרה אין סופית וחסומה קיים גבול חלקי |
|
|
נתונה הסדרה החסומה
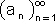 ז"א קיים חסם מלרע נאמר a וחסם מלעיל נאמר b
ז"א קיים חסם מלרע נאמר a וחסם מלעיל נאמר b אם כך כל איברי הסדרה שייכים לקטע [a,b]
ז"א a < a n < b נתבונן בשני הקטעים הסגורים [a, לפחות באחד מהם יש אין סוף איברים של הסדרה נאמר תכונה
p נבחר את הקטע בעל התכונה p , אם לשנהם התכונה p נבחר
את הימני ונסמנו נחלק שוב קטע זה לשניים באותה דרך ונקבל קטע [a2,b2] בעל תכונה p מתקיים a בסופו של דבר נקבל סדרת קטעים סדורים ז"א מתקיים
an לכל הקטעים תכונה p ואורכם
0 ע"פ הלמה של קנטור קיימת נקודה אחת ויחידה המקיימת
an בקטע [a1,b1] יש אנסוף איברים של הסדרה נבחר אחד מהם ונסמנו ב - an1 כך נבחר מכל קטע איבר יחיד עד שנקבל את הסדרה
an1.....ank
בקטעים [ak+1,bk+1] נבחר
ank+1 כך ש - nk < nk+1
אפשרי כי בקטע זה יש אין עם כך קיבלנו סדרה חלקית כאשר על פי הלמה של קנטור an על פי הסנדוויץ c
c גבול חלקי מש"ל
|
|
|
|
![]()
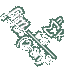
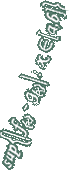



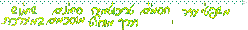


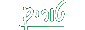
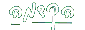
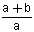 ] , [
] , [ 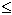 a1 < b1
a1 < b1 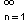 ([an,bn])
הכלואים זה בתוך זה
([an,bn])
הכלואים זה בתוך זה
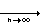
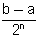 = an - bn
= an - bn
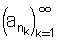
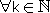
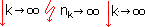
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©