
![]()
![]()
|
אזי לכל סדרה חלקית יש גבול ואותו
גבול (שווה לגבול של
|
|
|
הסבר: למקרה של גבול סופי
נאמר a, מחוץ לכל סביבת ולכן
גם מספר סופי של איברי סדרה חלקית כלשהי
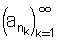
|
|
|
תהי ותהי נוכיח כי לסדרה החלקית יש גבול והוא a. יהי נתון a גבול הסדרה קיים n0 כך שלכל n > n0 n מתקיים
(1) עבור ההוכחה ש -a גבול הסדרה מ - (1) נקבל בפרט
|
|
|
תהיינה אשר איחודן הוא אזי ל -
|
|
|
לדוגמא: נתונה הסדרה (1) ...a1,a2,a3,a4 אם לסדרות החלקיות שלה: (2) ....a1,a3,a5 (3) ....a2,a4,a6 יש גבול ואותו גבול נאמר a אזי גם לסדרה (1) יש גבול והוא a
|
|
|
הסבר: מחוץ לסביבה יש מספר סופי של איברים מהסדרה (2) וגם יש מספר סופי של איברים מהסדרה (3) לכן מספר סופי ועוד מספר סופי שווה למספר סופי |
![]()





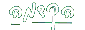
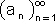 יש גבול במובן הרחב ( סופי או
יש גבול במובן הרחב ( סופי או 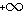 /-
)
/-
) 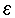
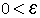 בפרט עבור
בפרט עבור 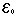 =
= 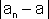
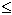 nk
nk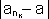
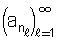 שתי סדרות
חלקיות של
שתי סדרות
חלקיות של הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©