
![]()
![]()
|
|
|
|
תהי נתונה סדרה כלשהי, |
|
|
|
![]()



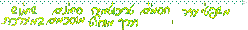


  |
||||||||||||
|
|
||||||||||||
|
|
|
|
||||||||||
 |
800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©
|
 |
||||||||||

 |
||||||||||||