
![]()
![]()
|
משפט 1 - גבול אינסופי גורר אי חסימות |
|
|
המשפט ההפוך אינו נכון ! |
|
|
נתון 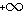
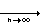 an
ויהי נתון 0 an
ויהי נתון 0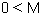 כיוון שהסדרה שואפת ל - 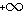 לכל
לכל 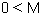 בפרט עבור M = M0 קיים n0 כך שלכל n ,n > n0 מתקיים: M0 < an יהי n1 = n0 + 1 מתקיים M0 < an0+1 פרושו שהסדרה אינה חסומה מלעיל . |
|
|
נתבונן בסדרה ........1,1,2,1,3,1,4 ניתן לראות כי הסדרה אינה חסומה מלעיל וכן אינה שואפת לאין סוף (לא כמעט כל האיברים נמצאים באינסוף - ישנם אינסוף איברים ששוים ל- 1) |
|
|
משפט 2 - גבול אינסופי גורר אי חסימות |
|
|
הוכחה זהה !!! |
|
|
|
|
|
יהי נתון 0
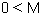 (רוצים להוכיח כי לכל M הדבר מתקיים ולכן אי אפשר לבחור M
(רוצים להוכיח כי לכל M הדבר מתקיים ולכן אי אפשר לבחור M אלא הוא נתון מראש) לפי הנתון 0 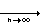 an ולכן לכל
an ולכן לכל 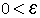 בפרט עבור
בפרט עבור 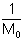 = = 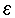
קיים n0 כך שלכל n ,n > n0 מתקיים: 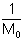 < | 0 - an< | an
< | 0 - an< | an נקבל 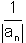 > M וזה
מתקיים לכל n > n0 , n > M וזה
מתקיים לכל n > n0 , n |
|
|
יהי נתון 0 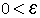
לפי הנתון 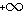 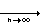 |an| ולכן לכל
|an| ולכן לכל 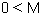 בפרט עבור
בפרט עבור 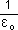 =
M0 =
M0קיים n0 כך שלכל n ,n > n0 מתקיים: |an| < 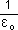 נקבל 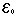 > > 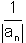 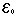 > >  0 -
0 - 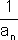  >
> 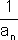 |
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©


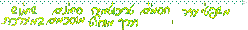


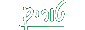
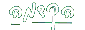
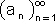 בעלת גבול
בעלת גבול 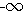 אזיי
היא אינה חסומה מלרע
אזיי
היא אינה חסומה מלרע 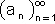 גבול 0 כאשר 0
גבול 0 כאשר 0  n
an
n
an
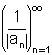 גבול
גבול 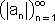 גבול 0 כאשר 0
גבול 0 כאשר 0 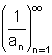 גבול
גבול  הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©