
![]()
![]()
|
|
|
|
|
|
|
נגדיר סדרה קבועה 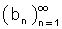 כך ש - b = bn , n
כך ש - b = bn , n לסדרה זו יש גבול והוא שווה ל - b ע"פ משפט 1 (שמירת יחסים) קיים n0 כך שלכל n > n0 , n מתקיים: an < bn < b |
|
|
נתון כי ל - 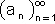 גבול a
גבול aול - 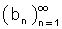 גבול b
גבול bבנוסף נתון כי קיים n0 כך שלכל n > n0 מתקיים: (1) an 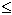 bn
bn אזי a 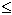 b
b |
|
|
נתון כי ל - 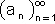 גבול a
גבול aויהי b מספר בנוסף נתון כי קיים n0 כך שלכל n > n0 מתקיים: an 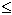 b
b אזי a 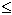 b
b |
|
|
bn סדרה קבועה שאבריה b ולפי משפט 3 (שמירת
יחסים) נקבל כי an 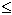 bn bn a 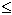 b b |
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©


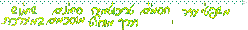


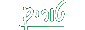
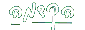
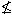 b ע"פ הטריכוטומיה b < a
b ע"פ הטריכוטומיה b < a הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©