תהיינה ו - שתי סדרות המקיימות

(1) a_n a_n+1 < b_n+1 b_n         (ז"א a_n עולה ו - b_n יורדת )

(2) 0 = (b_n - a_n)

אזי קיימת נקודה אחת ויחידה כך ש - b_n c a_n    

הסבר: לכל סדרה אפסה של קטעים סגורים הכלואים

זה בתוך זה יש נקודה משותפת אחת ויחידה .

סדרה עולה ו - סדרה יורדת

מתקיים a₁ .... a_n a_n+1 < b_n+1 b_n .... b₁

ולכן חסומה מלעיל ע"י b₁ ו - חסומה מלרע ע"י a₁

לכן לשתי הסדרות יש גבול נרשום:   c₂ = b_n   וכן   c₁ = a_n

ע"פ משפט אי שוויונים בסדרות מתקיים (3) c₂ b_n ו - a_n c₁     

נוכיח כי c₂ = c₁

ואמנם 0 =( c₂ - c₁ = b_n - a_n = (b_n - a_n

         c₂ = c₁ c₂ - c₁ = 0

נסמן את הערך המשותף של c₁ ו- c₁ ע"י c

מ - (3) קיבלנו כי b_n c a_n    

נוכיח כי c הנ"ל יחידה :

נניח בשלילה כי קיימת c` נקודה כלשהי כך ש -b_n c' a_n    
                                                                       
                                                             -b_n -c' -a_n
            וכן                                                  b_n c a_n

אחרי חיבור נקבל :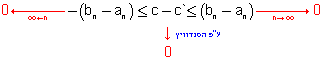          

0 = (c` - c)

c - c` = c - c` = 0

ולכן c` = c

                                                    מש"ל