
![]()
![]()
|
|
|
|
ידוע אי שוויון ברנולי: א. 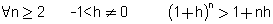 ב. 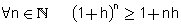 טענה 1: הסדרה חסומה מלרע - 2 <  + 2 = + 2 =  (
1+ n ) + 1 (
1+ n ) + 1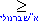 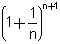 טענה 2: הסדרה יורדת אפילו ממש - נסמן 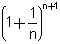 = bn ונוכיח כי bn+1
= bn ונוכיח כי bn+1
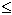 bn
או 1 bn
או 1 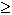
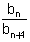
 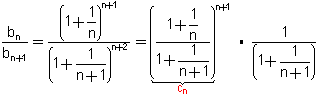 מספיק להוכיח כי cn 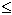
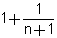
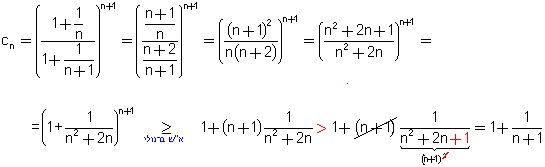 קיבלנו cn < 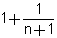 ע"פ משפט 1 - לסדרה 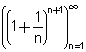 יש גבול המסומן e והוא נקרא מספר אויילר
יש גבול המסומן e והוא נקרא מספר אויילר ע"פ משפט 2 - החסם התחתון של הסדרה הנ"ל הוא הגבול ולכן שווה ל - e בטענה 1 ראינו כי 2 הוא חסם מלרע ולכן e 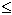 2
2נחשב את האיבר החמישי 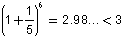
כוון שהסדרה יורדת נקבל e > 3 אם כך 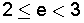
מספר אויילר הוא מספר אי רציונלי ואפילו טרנסצדנטלי 2.718181828 = e |
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©


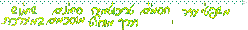


 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©