
![]()
![]()
|
משפט 1 - מונוטונית חסומה בעלת גבול הוכחה: |
|
|
תהי 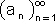 סדרה עולה ז"א : an
סדרה עולה ז"א : an 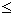 an+1
an+1 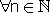 וכן חסומה מלעיל .
וכן חסומה מלעיל .ז"א ע"פ אכסיומת השלמות יש לסדרה חסם עליון יהי a. א. an 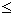 a
a 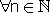 ב. לכל 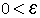 קיים n1 כך ש - a -
קיים n1 כך ש - a - 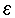 < an1
< an1 טענה :- a גבול הסדרה ואמנם יהי נתון 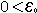 ע"פ ב. לכל 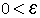 בפרט עבור
בפרט עבור 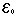 = =
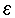 קיים n1
כך ש - (1) a - קיים n1
כך ש - (1) a - 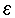 < an1
< an1 לכל n > n1 כוון שהסדרה עולה (2) an1 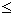 an
anמ - א. קיבלנו (3) an 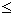 a
a 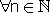 נקבל כי לכל n n < n1 מתקיים: (3) (2) (1) 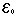 + a - + a - 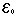 < an1
< an1 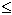 an
an 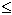 a < a
a < a 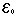 + a - + a - 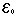 <
an < a <
an < a מש"ל |
|
|
משפט 2 - מונוטונית חסומה בעלת גבול הוכחה: |
|
|
הוכחה זהה
|
|
|
משפט 3 אינה חסומה גורר גבול לא קיים: |
|
|
תהי נתונה
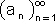 סדרה עולה שאינה חסומה מלעיל ונוכיח כי שואפת ל -
סדרה עולה שאינה חסומה מלעיל ונוכיח כי שואפת ל - 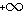
יהי נתון M0 > 0 כוון שהסדרה אינה חסומה מלעיל לכל 0 < M בפרט עבור M = M0 קיים n1 כך ש- (1) M0 < an1 לכל an1 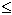 an (2) n > n0 ,
n (הסדרה עולה)
an (2) n > n0 ,
n (הסדרה עולה) ולכן לכל n > n0 , n (ע"פ טרניטביות יחס הסדר) M0 < an |
|
|
משפט 4 אינה חסומה גורר גבול לא קיים: |
|
|
הוכחה זהה |
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©




 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©