
![]()
![]()
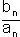 =
= 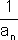 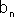 ולכן ע"פ המשפט לגבי גבול מכפלה והמשפט הקודם
ולכן ע"פ המשפט לגבי גבול מכפלה והמשפט הקודם
נקבל כי גבול הסדרה  הוא
הוא 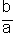 =
=  b b |
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©




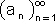 בעלת גבול a כאשר 0
בעלת גבול a כאשר 0  a
a 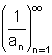 יש גבול והוא
יש גבול והוא 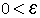
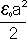 =
= 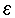 קיים 'n0
כך שלכל n > 'n0 מתקיים
קיים 'n0
כך שלכל n > 'n0 מתקיים 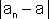
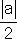 =
= 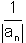 >
> 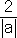

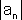 >
> 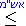
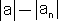
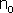 , '
, '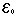 =
=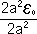 =
= 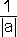 >
> 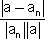 =
=
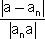 =
= 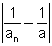
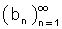 סדרה בעלת
גבול b
סדרה בעלת
גבול b הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©