
![]()
![]()
|
נתונה הסדרה
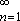 {an},
יהי L גבול הסדרה {an},
יהי L גבול הסדרה לכל 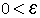 בפרט עבור
בפרט עבור 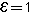 קיים n0 כך שלכל n > n0 מתקיים:
קיים n0 כך שלכל n > n0 מתקיים:
נקבל
נסמן ולכן
נסמן נקבל
ע"פ ערך מוחלט נקבל כי |
|
|
|
|
|
הערה: לא לכל סדרה חסומה
יש גבול למשל לסדרה החסומה...1-...1-,1,1-,1 אין |
|
|
|
|
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©


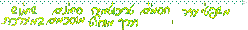


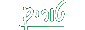
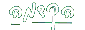
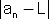
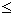
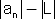

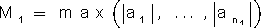
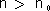
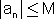
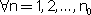
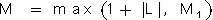
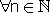
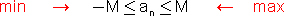
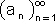 חסומה ול-
חסומה ול-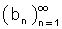 יש
גבול 0
יש
גבול 0 יש גבול והוא 0.
יש גבול והוא 0. 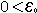
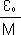 =
=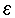 קיים 'n0 כך ש-
קיים 'n0 כך ש- 0-
0-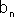
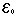 הנתון נבחר 'n0 = n0
הנתון נבחר 'n0 = n0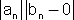 =
= 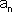
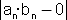
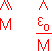
 הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©