
![]()
![]()
|
יה נתון 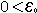 a גבול הסדרה 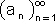 ולכן ע"פ הגדרת גבול סדרה לכל
ולכן ע"פ הגדרת גבול סדרה לכל 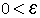
בפרט (אני יודע כי קיים גבול לכל 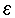 ולכן אני יכול לבחור ) עבור
ולכן אני יכול לבחור ) עבור 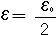
קיים 'n0 כך שלכל n ' 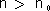 מתקיים
מתקיים 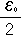 >
> 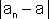 b גבול הסדרה 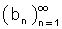 ולכן ע"פ הגדרת גבול סדרה לכל
ולכן ע"פ הגדרת גבול סדרה לכל 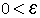
בפרט (אני יודע כי קיים גבול לכל 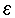 ולכן אני יכול לבחור ) עבור
ולכן אני יכול לבחור ) עבור 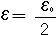 קיים ''n0 כך שלכל n '' 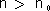 מתקיים
מתקיים 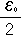 >
> 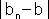 נסמן ( n0 = Max(''n0,'n0. n0 הוא המתאים ל - 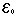 הנתון להוכחת גבול סדרת הסכום ,ואמנם, לכל n המקיים
הנתון להוכחת גבול סדרת הסכום ,ואמנם, לכל n המקיים 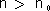 מתקיים
בפרט ' מתקיים
בפרט '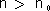 ולכן
ולכן 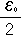 >
> 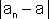 נכון
נכון וכן '' 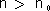 ולכן ולכן
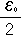 > > 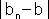 נכון
נכון 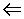  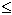 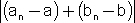 =
=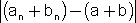 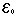 =
= 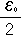 + +
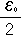 > > 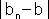 +
+ 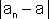
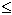
קיבלנו כי 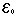 >
> 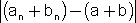 מש"ל.
מש"ל. |
|
|
|
|
|
ההוכחה זהה להוכחה עבור סכום סדרות.
|
![]()

800X600 כל הזכויות שמורות למערכת המידע האקדמית איתן הצפיה
מומלצת ברזולציה ©


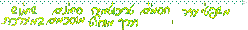


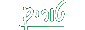
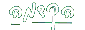
 קיים גבול והוא
קיים גבול והוא  קיים גבול והוא
קיים גבול והוא  הצפיה
מומלצת ברזולציה ©
הצפיה
מומלצת ברזולציה ©