עמוד זה מכיל דוגמאות לגבי הנושאים הבאים:
1. ביטויים מתמטיים
2. שימושים ויישומים שונים
![]()
בסעיף זה נתאר דוגמאות לפונקציות מתמטיות שניתן להציג באמצעות התוכנית.
נתחיל במספר דוגמאות פשוטות, ונגיע לדוגמאות מורכבות יותר. מומלץ לנסות את הדוגמאות
בתוכנית!
דוגמאות פשוטות:
- פולינום: 2x^2-5x+1
- פונקציה רציונאלית: (x-1)/(x^2+1)
- פונקציות טריגונומטריות: sin(2x)-cos(pi x)^2
- אקספוננט: e^(x^2/2), ואפשר גם:
exp(x^2/2)
דוגמאות מורכבות:
- "הדבקה" של פונקציות, לדוגמא:
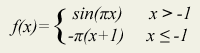
ניתן להשתמש בפונקצית heaviside על-מנת לבטא פונקציות כאלה. פונקצית heaviside מחזירה 0 לכל x<0 ו- 1 לכל x>=0. הפונקציה מהדוגמא תיכתב בצורה:
-pi(x+1)*heaviside(-(x+1)) +
sin(pi x)*heaviside(x+1)
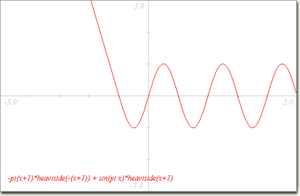
- ניתן "להרוג" חלק מפונקציה ע"י הכפלה בפונקציה rect, המחזירה 1 לכל
|x|<=1 ו- 0 אחרת.
לדוגמא:
sin(pi x)*rect(x/2). ניתן להשתמש ב- rect גם ל"הדבקה" כמו בדוגמא הקודמת
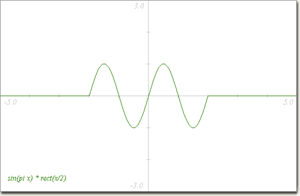
- אפשר להשתמש ב- gaussian(x) כקיצור ל-
exp(-x^2/2) (זוהי פונקצית ההתפלגות הנורמאלית הסטנדרטית של Gauss)
![]()
כאן נתאר מספר יישומים מתמטיים "חינוכיים" של צייר הפונקציות.
- מציאת שורשים של פונקציה (או חיתוך עם הצירים).
הקלידו את הפונקציה שברצונכם לבדוק ושנו את ה-Zoom כך שתראו את נקודות החיתוך. כעת הזיזו את העכבר לנקודה וכך תוכלו לראות את שיעורי ה-X וה-Y שלה בתחתית המסך.
לדוגמא: כמה פתרונות יש למשוואה x^3-2x+1=0 ? מהם (בקירוב)? - קירוב מספרים אי-רציונאליים.
על-מנת לקרב את המספר pi, לדוגמא, יש למצוא את השורש של הפונקציה sin(x).
על-מנת לקרב את sqrt(2), יש למצוא את השורש של
x^2-2.
התמקדו ע"י העכבר בנק' הרצויה - מציאת נקודות קיצון של פונקציה.
ציור גרף הפונקציה נותן אפשרות למצוא (בקירוב) את נקודות הקיצון המקומיות והמוחלטות של הפונקציה
